概率编程(Probabilistic programming)的PyMC3实现

概率编程中的概率是指概率推理，特指贝叶斯方法里的概率及其求解；编程是指通过计算机编程语言(如Python)去实现建模和求解。其中关键是变分推断(Variational inference)技术。PyMC3是Python中实现概率编程的模块，它利用了新一代的MCMC抽样算法(如NUTS)，因而计算速度快，使得概率编程容易实现。本文举了多个例子，其中线性回归的例子中详细介绍了pymc3的用法。

1.Windows/Python3.5安装pymc3和theano

step 1: pip3 install mingw # 利用pip或conda安装的mingw，而不是独立安装的mingw
把mingw模块的路径加入系统PATH:
D:\your-path\Anaconda3\MinGW\bin;
D:\your-path\Anaconda3\MinGW\x86_64-w64-mingw32\lib;
如果独立安装的mingw也在PATH中，需要删除。

step 2: pip3 install theano
打开Python测试代码：
import theano
theano.test()

step 3：pip3 install pymc3
python中测试：
import pymc3

2.拟合分布

问题：x=np.array([10, 20, 30, 29, 28, 30, 32, 16, 24, 26, 32, 40, 50, 31, 38, 35, 28])
假设x符合Poisson分布，求参数mu(即lambda)。这是一个最简单的模型，我们分别用最传统的极大似然法和贝叶斯方法去拟合Poisson分布。

极大似然法(MLE)：

1
2
3
4
5
from scipy import stats, optimize
def logprod(mu):
    return np.sum(-1*stats.poisson.logpmf(x,mu)) #-1把求解极大值变为极小值
result=optimize.minimize_scalar(logprod)
print(result)  # x=29.3

MLE只能给出一个点估计，无法对精确性进行评估

贝叶斯方法：

1
2
3
4
5
6
7
8
import pymc3 as pm
with pm.Model() as m1:      # 建立模型
  mu=pm.Uniform('mu',lower=0,upper=100)  # 指定求解参数的分布
  x_obs=pm.Poisson('x',mu=mu,observed=x)  # 这里求解似然值，而不是后验分布
  start=pm.find_MAP()  # 参数初猜
  step=pm.Metropolis() # 指定抽样方法
  trace=pm.sample(10000, start=start, step=step, cores=1) # 抽样过程
  # cores=1为了pymc3在Windows下正常使用

注意：开始我没加cores参数，运行时得到错误：ValueError: must use protocol 4 or greater to copy this object; since getnewargs_ex returned keyword arguments。google了才知晓(墙!)，其原因是pymc3中默认启动多线程并行计算，需要pickle模块。而pickle适合Linux，在Windows环境下会有诸多问题(muliprocessing模块在windows下使用也有此问题)。最简单的解决方法是添加参数cores=1，即trace = sample(2000,start=start, step=step, cores=1)，不耽误当前的练习，但这样会放弃多核计算的方便性。

模型收敛的判断和结果提取：

1
2
3
pm.traceplot(trace)
pm.autocorrplot(trace)
pm.summary(trace)  # x=29.4, 95%CI:26.7~31.8

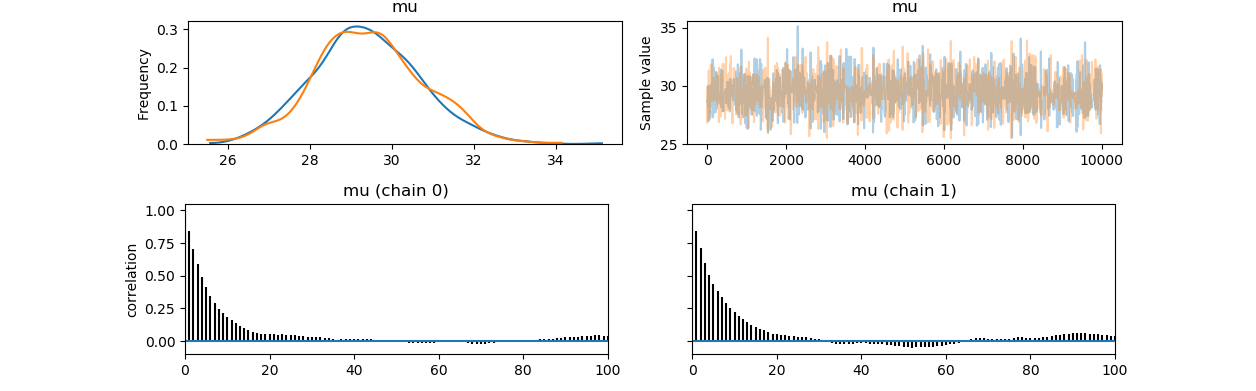
3.分层拟合：分层方法已知时(独立模型思路)

例如上面拟合分布的例子，假设这批数据是已知两个群体的，其对应的分组为group=np.array([1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2])。
解决方案很简单，因为每个组的参数各自独立，所以通过一个循环即可解决。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
traces={}
for i in [1,2]:
  with pm.Model() as model:
    mu=pm.Uniform('mu',lower=0,upper=100)
    x_obs=pm.Poisson('x',mu=mu,observed=x[group==i])
    start=pm.find_MAP()
    step=pm.Metropolis()
    trace=pm.sample(10000, start=start, step=step, cores=1)
    traces[i]=trace
#显然这儿用多线程技术更好
pm.sumary(traces[1])
#结果：
     mean    sd  mc_error  hpd_2.5  hpd_97.5    n_eff  Rhat
mu  24.49  1.65      0.04    21.48     27.98  2389.11   1.0
pm.sumary(traces[2])
#结果：
     mean    sd  mc_error  hpd_2.5  hpd_97.5    n_eff  Rhat
mu  35.09  2.09      0.04    30.76     38.84  2227.11   1.0

4.分层拟合：分层方法已知时(融合模型思路)

上一个例子是独立建模的例子。但分层太多时，有些组个体数量很少，估计值有较大的不确定性(每个组分别通过hist函数画频数图、即可看出实际分布是否理论分布有差距)。此时，样本容量太小带来错误的结论。这时可以采取一种叫局部融合的思路。因为整体的数据量大，可以把每个组的后验预测分布联合起来，希望得到的分布和观测数据分布近似，顾名思义“融合”。加上任意的分布节点，对于概率编程/pymc3是很容易的。

独立模型是：(i为group)
yi~Poisson(μi)
μi=Uniform(0,100)

融合模型是：每个组的μi(称之为参数)受共同的超参数(又称融合参数)制约
yi~Poisson(μi)
μi=Gamma(μ,σ)
μ=Uniform(0,100)
σ=Uniform(0,60)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
with pm.Model() as m1:
    hyper_mu=pm.Uniform('hyper_mu',lower=0,upper=100)
    hyper_sd=pm.Uniform('hyper_sd',lower=0,upper=60)
    mu=pm.Gamma('mu', mu=hyper_mu, sd=hyper_sd, shape=2)
    #shape=2提示mu是含有两个值的list，对应两个组的mu
    #μ1和μ2不可以单独定义，因为融合模型的需要
    x_obs=pm.Poisson('x',mu=mu[group-1],observed=x)
    # group值为1,2，但mu的index从0开始
    start = pm.find_MAP()
    step = pm.Metropolis()
    trace=pm.sample(10000,step=step, cores=1)
pm.summary(trace)
结果：
           mean     sd  mc_error  hpd_2.5  hpd_97.5    n_eff  Rhat
hyper_mu  41.07  16.40      0.47    16.33     78.06   982.00   1.0
hyper_sd  24.67  16.09      0.51     2.96     55.60   876.66   1.0
mu__0     24.58   1.65      0.04    21.44     27.84  1544.44   1.0
mu__1     34.90   2.04      0.05    31.17     39.04  1841.49   1.0

5.分层拟合：分层方法未知时(需求解分层的截断值)

这里涉及到了确定性随机变量(Deterministic random variable)的知识，因为这个截断值是random variable，但是deterministic(表面上看这两个词似乎矛盾，更多理解参考pymc3 tutorial)。这里模型混合了Stochastic random variable和Deterministic random variable，这大大增加了pymc3的应用范围。

问题：已知1851到1962年每年的矿难数，理论上服从Poisson分布。但从某一年开始矿难数下降，即Possion分布的参数改变了，求哪一年？

1
2
3
4
5
6
7
8
data = np.ma.masked_values([4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
                            3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
                            2, 2, 3, 4, 2, 1, 3, -999, 2, 1, 1, 1, 1, 3, 0, 0,
                            1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
                            0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
                            3, 3, 1, -999, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
                            0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1], value=-999)
years = np.arange(1851, 1962)

1
2
3
4
5
6
7
8
9
10
11
with pm.Model() as m2:
    switchpoint = pm.DiscreteUniform('switchpoint', lower=years.min(), upper=years.max(), testval=1900)
    early_rate = pm.Exponential('early_rate', 1)
    late_rate = pm.Exponential('late_rate', 1)
    rate = pm.math.switch(switchpoint >= years, early_rate, late_rate)  #这儿是确定性随机变量
    disasters = pm.Poisson('disasters', rate, observed=data)
    trace = pm.sample(10000, cores=1)  # 自动判断step=pm.Metropolis()
pm.traceplot(trace)
m2.vars  # 查看模型中的变量
pm.summary(trace)  # 结果swithpoint=1889, 95%CI:[1885,1894]
6.线性回归：

这里更详细的介绍pymc3的用法。这里的线性回归是只有Stochastic random variable的模型，即不涉及确定性随机变量(Deterministic random variable)(比如分层)

问题:

1
2
3
4
5
6
7
import numpy as np
x1=np.random.randn(100)
x2=np.random.randn(100)
x3=np.random.randn(100)
e=np.random.randn(100)/10
beta0,beta1,beta2=1,2,3
y=beta0+beta1*x1+beta2*x2+e     #故意不加入x3，看能否检测出来

假设y~x1+x2+x3，求解系数(点值估计和标准差)，预期x3系数为0

1
2
3
4
5
6
7
8
9
10
11
from pymc3 import Model
from pymc3 import Normal, HalfNormal
with Model() as m1:
   beta0=Normal('beta0',mu=0,sd=10)  # 给出参数的先验分布(估计值)，
   beta1=Normal('beta1',mu=0,sd=10)  # 可以把四个参数定义成一个list，例如：
   beta2=Normal('beta2',mu=0,sd=10)	 # beta=Normal('beta',mu=0,sd=10,shape=4)
   beta3=Normal('beta3',mu=0,sd=10)
   sigma=HalfNormal('sigma',sd=1)
   mu=beta0+beta1*x1+beta2*x2+beta3*x3
   y_obs=Normal('y',mu=mu,sd=sigma,observed=y)

模型已经建好了，求解模型的方法有两种MAP法和抽样法。前者可以后者提供参数值的初猜，当然也可以不用。后者可以进行多轮模拟，前面的模拟(最后的取值，如trace[-1])为后面的模拟提供初猜。

Maximum a posteriori method:
MAP法使用了数值优化方法，计算速度快，但只能给出一个点估计(不能得到区间估计)。而且当选择取的分布不能代表模型时，其结果可能有错误。默认使用Broyden–Fletcher–Goldfarb–Shanno (BFGS)优化算法，还可以使用scipy中的。

1
2
3
4
5
6
7
8
9
10
from pymc3 import find_MAP
res=find_MAP(model=m1)   #  find_MAP(model=m1, fmin=scipy.optimize.fmin_powell)
print(res)
结果：
{'beta0': array(0.99203671),
 'beta1': array(2.01214997),
 'beta2': array(3.00993282),
 'beta3': array(0.01450897),
 'sigma': array(0.10374381),
 'sigma_log_': array(-2.26583075)}

Sampling method:
基于模拟的方法，即MCMC。具体实现MCMC的抽样方法有NUTS(连续变量), Metropolis(多分类变量), BinaryMetropolis(二分类变量), Slice, HamiltonianMC。

1
2
3
4
5
6
7
8
9
10
from pymc3 import NUTS, sample
from scipy import optimize
with m1:
    # 通过MAP法初猜参数
    start=find_MAP(fmin=optimize.fmin_powell)
    # 选择采样方法
    step=NUTS(scaling=start)
    # 2000次抽样
    trace=sample(2000, start=start, step=step,cores=1)

如果需要的话可以多轮

1
2
with m1:
	trace2=sample(2000, start=trace[-1], step=step,cores=1)

结果：

1
2
3
4
5
6
7
8
9
10
11
print(trace['beta0'])
pymc3.traceplot(trace)     # 根据波动程度判断是否收敛
pymc3.autocorrplot(trace)  # 根据自相关判断是否收敛
pymc3.summary(trace)
#结果：
         mean      sd  mc_error  hpd_2.5  hpd_97.5       n_eff    Rhat
beta0  0.9919  0.0111    0.0001   0.9699    1.0135  18582.6262  1.0000
beta1  2.0120  0.0128    0.0001   1.9880    2.0379  21422.0932  1.0000
beta2  3.0099  0.0111    0.0001   2.9878    3.0319  21225.4985  1.0000
beta3  0.0145  0.0112    0.0001  -0.0071    0.0369  20549.0559  1.0000
sigma  0.1073  0.0079    0.0000   0.0924    0.1231  28215.3758  1.0001

其中HPD是Highest Posterior Density，计算相当于频率派的可信区间。结果给出了95%的HPD区间: [hpd_2.5, hpd_97.5]

7.t检验：

两组x1和x2，判断均数是否有差别。产生随机数：

1
2
3
4
from scipy import stats
import pymc3 as pm
x1=stats.norm(0,1).rvs(50)
x2=stats.norm(1,1).rvs(50)

频率派的t检验方法：

1
2
3
4
ans=stats.ttest_ind(x1,x2)
print("P value is: %f"%(ans.pvalue))
结果：
'P value is: 0.000292'

贝叶斯方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
with pm.Model() as m1:
  x1_mean=pm.Normal('x1_mean',mu=np.mean(x1),sd=10)
  x2_mean=pm.Normal('x2_mean',mu=np.mean(x2),sd=10)
  x1_sd=pm.Uniform('x1_sd',lower=0,upper=10)
  x2_sd=pm.Uniform('x2_sd',lower=0,upper=10)
  x1_lam=x1_sd**-2
  x2_lam=x2_sd**-2
  nu=pm.Exponential('nu',1/29)
  x1_obs=pm.StudentT('x1',mu=x1_mean,lam=x1_lam,nu=nu,observed=x1)
  x2_obs=pm.StudentT('x2',mu=x2_mean,lam=x2_lam,nu=nu,observed=x2)
  diff_mean=pm.Deterministic('diff_mean',x1_mean-x2_mean)
  diff_sd=pm.Deterministic('diff_sd',x1_sd-x2_sd)
  effect_size=pm.Deterministic('effect_size',diff_mean/np.sqrt((x1_sd**2+x2_sd**2)/2))
with m1:
  trace=pm.sample(10000,cores=1)
pm.traceplot(trace)
pm.summary(trace).round(4)
pm.posteriorplot.plot_posterior(trace['effect_size'])
结果：
                mean       sd  mc_error  hpd_2.5  hpd_97.5       n_eff  Rhat
x1_mean       0.2699   0.1548    0.0010  -0.0386    0.5671  23057.4224   1.0
x2_mean       1.0360   0.1482    0.0011   0.7569    1.3400  19007.0775   1.0
x1_sd         1.0571   0.1199    0.0009   0.8330    1.2957  19998.3161   1.0
x2_sd         0.9985   0.1109    0.0008   0.7909    1.2254  19406.9874   1.0
nu           39.5042  30.4867    0.2202   2.8984  101.3137  20087.7724   1.0
diff_mean    -0.7661   0.2148    0.0014  -1.1874   -0.3558  20680.9116   1.0
diff_sd       0.0586   0.1588    0.0011  -0.2524    0.3704  22313.2461   1.0
effect_size  -0.7474   0.2151    0.0013  -1.1884   -0.3523  21286.4975   1.0

x1和x2的均数、方差的估计值除了x1的均属其它还是很准确的。结果effect size的95%HPD为[-1.1884,-0.3523]，effect_size等于0的概率小于0.05，即两组间有差别。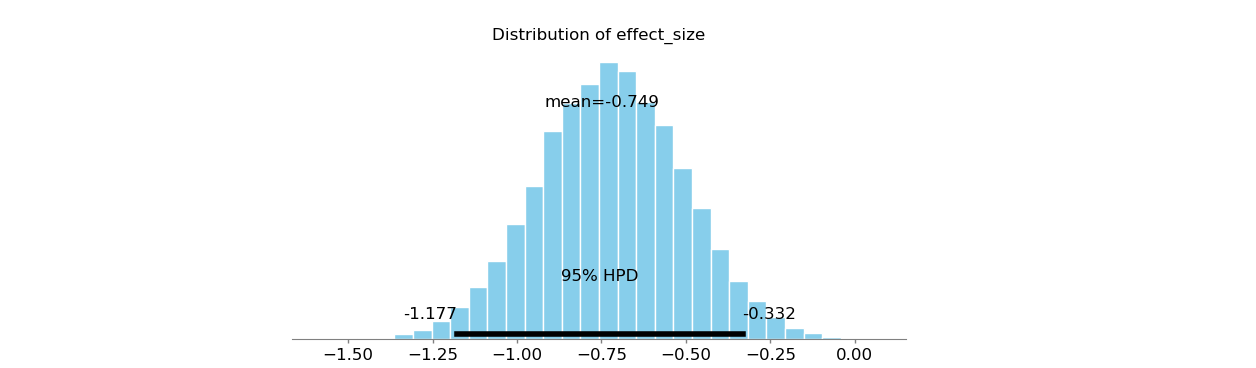

8.知识扩展：自定义确定性变量(Arbitrary deterministics):

pymc3调用了theano实现其变分推理，所以这儿也用theano自定义函数。
方法1：同前面矿难的例子
方法2：theano的as_op装饰器，见下：

1
2
3
4
5
6
7
8
9
10
11
12
13
import theano.tensor as tt
from theano.compile.ops import as_op
@as_op(itypes=[tt.lscalar], otypes=[tt.lscalar])
def crazy_modulo3(value):
    if value > 0:
        return value % 3
    else :
        return (-value + 1) % 3
with pm.Model() as m3:
    a = pm.Poisson('a', 1)
    b = crazy_modulo3(a)

9.知识扩展：pymc3预定义的回归模型

pymc3预定义了Linear regression model和Logistic regression model，可以不必自己构建model。用起来如同R语言的建模一样方便。

假设一般线性回归模型:y~x1+x2

1
2
3
4
5
6
7
import pandas
df = pandas.DataFrame({'x1': x1, 'x2': x2, 'y': y})
with pm.Model() as glm:
    pm.glm.GLM.from_formula('y ~ x1 + x2', df)
    trace = pm.sample(10000,cores=1)
pm.summary(trace)

假设Logistic回归模型:logit(y)~x1

1
2
3
4
5
df = pandas.DataFrame({'x1': x1, 'y': Y > np.median(Y)})
with pm.Model() as logistic:
    pm.glm.GLM.from_formula('y ~ x1', df_logistic, family=pm.glm.families.Binomial())
trace = pm.sample(10000,cores=1)
pm.sumary(trace)

赏

谢谢你请我吃糖果

支付宝
微信

扫一扫，分享到微信

微信分享二维码
这不是科学的乐园<br>而是科学的森林<br>无处不充满着引人入胜的奥秘<br>Email:sunnysean@qq.com<br>